
NộI Dung
- Luật của Zipf giải thích
- Thí nghiệm cơ bản
- Luật của Zipf trên thị trường hơi nước
- Chúng ta có thể học được gì về Steam?
- Kết luận
Cách đây không lâu, một người bạn của tôi đề nghị tôi xem video Vsauces về luật của Zipf, nguyên tắc của Pareto và sự xuất hiện bí ẩn của họ xung quanh chúng ta. Dưới đây là một lời trêu ghẹo để thu hút sự chú ý của bạn - 80% tất cả mọi người sống ở 20% các thành phố nổi tiếng nhất; 80% tất cả đất đai thuộc về 20% địa chủ giàu có nhất; 80% tất cả rác nằm trên 20% đường phố hàng đầu - theo dự đoán của luật Zipf và nguyên tắc Paretos.
Không đủ? Chà, như tôi đã phát hiện ra ngày hôm qua, lỗ thỏ không dừng lại ở đó ... Đầy hoài nghi, tôi quyết định xem mọi người dành bao nhiêu thời gian để chơi các trò chơi trên Steam ... Chà. 80% thời gian của mọi người được dành để chơi 20% các trò chơi phổ biến nhất ... Thú vị không? Vâng, đọc tiếp, có nhiều hơn cho câu chuyện này.
Đồng hồ điểm hơn 20 phút, nỗ lực của Vsauces thật tuyệt vời và giải thích rất nhiều nội dung hình ảnh lớn về Zipf, tuy nhiên anh ấy rất ngại cho chúng tôi thấy cơ chế cốt lõi được nhiều người tin tưởng để góp phần giải thích tại sao Zipf hoạt động như thế nào. Vì vậy, trước khi chúng tôi tiếp tục, tôi muốn giải thích ngắn gọn về điều đó.
Luật của Zipf giải thích
Có một số cách khái niệm để giải thích trực giác đằng sau nguyên tắc 20/80. Ví dụ tốt nhất, theo tôi, là một ví dụ về các miệng hố Mặt trăng.
Thí nghiệm cơ bản
Vì vậy, hãy tưởng tượng nếu bạn muốn, rằng có một Mặt trăng chưa được chạm tới - một bề mặt hoàn toàn nhẵn. Bây giờ, giả sử có một số tiểu hành tinh có kích thước ngẫu nhiên đâm vào Mặt trăng willy-nilly. Khi tiểu hành tinh đầu tiên hạ cánh, nó để lại một miệng núi lửa. Bây giờ một người khác đánh, để lại một miệng núi lửa ở nơi khác. Mỗi miệng núi lửa là một phần của tổng diện tích bề mặt, do đó, có khả năng tiểu hành tinh ngẫu nhiên tiếp theo sẽ đâm sát vào miệng núi lửa hiện có và tham gia với nó, tạo thành một nhóm. Cơ hội của một tiểu hành tinh mới đâm vào một miệng hố nhất định sau đó tỷ lệ thuận với các miệng hố và các tiểu hành tinh có kích thước hiện có. Điều này có nghĩa là tiểu hành tinh ngẫu nhiên tiếp theo có nhiều khả năng tham gia nhóm lớn nhất hiện có, khiến nó còn lớn hơn nữa. Một loại quá trình tích lũy, sau đó tạo ra một cơ chế giàu nghèo làm giàu nghèo hơn.
Hãy ghi nhớ điều này, bởi vì đó được cho là lời giải thích chung cho "tại sao" luật Zipfs hoạt động với tính phổ quát bí ẩn như vậy. Ví dụ về tiểu hành tinh khá đơn giản, tuy nhiên câu hỏi đặt ra là điều gì sẽ xảy ra qua nhiều lần lặp lại
Một chút hoang mang?
Vâng, tôi đã làm một gif để lái xe điểm ban đầu này về nhà. Lưu ý! đồ thị sẽ được thảo luận sau, chỉ cần thử và hình dung thử nghiệm.

Nếu chúng ta quan sát Mặt trăng thực tế, hóa ra, khi lượng tiểu hành tinh tăng lên một lượng lớn, đường kính miệng núi lửa quan sát tăng lên để 20% miệng hố lớn nhất tiếp cận 80% diện tích bề mặt.
Vì vậy, khi chúng ta đến nhiều tiểu hành tinh hơn, việc phân phối các nhóm phổ biến nhất đến phổ biến nhất tiếp cận một số loại "phân phối lý tưởng" với tài sản 20/80 này - phân phối Pareto. Nếu bạn làm toán, hóa ra (nói chung), nếu nhóm lớn nhất có kích thước N, thì nhóm lớn thứ hai là khoảng cỡ N / 2, N / 3 thứ ba, v.v. Đây được gọi là Luật của Zipf. Điều kỳ lạ là phân phối Pareto và Luật của Zipf hoạt động cho một lượng lớn các yếu tố (tiểu hành tinh) và các nhóm (cụm miệng núi lửa). Tất nhiên, có những xiên và xáo trộn ngẫu nhiên, nhưng xu hướng chung là không thể phủ nhận.
Tôi hy vọng bạn có thể thấy các tiểu hành tinh có khả năng đâm vào các miệng hố lớn trên Mặt trăng kết nối với các thành phố hấp dẫn hơn như thế nào, nếu đã có nhiều người sống trong đó. Tuy nhiên, người ta phải nhận ra, các thành phố cách xa các "nhóm" duy nhất hành xử theo Zipf.
Dưới đây là một số ví dụ từ nghiên cứu của Mark Newmans về phân phối Pareto. Lưu ý! Các biểu đồ nằm trong thang đo log-log giúp làm mịn hình dạng hyperbol của các đường cong, thể hiện mối quan hệ gần như tuyến tính.
Ban đầu y = aX ^ (- b)
Nhật ký của cả hai bên => log y = log a - b log X
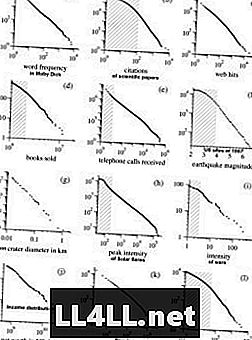
Điều thú vị là, xu hướng tương tự cũng được hiển thị bởi các giáo phái tôn giáo ... Tài sản chung của hầu hết các hiện tượng này chỉ đơn giản là xu hướng "nhóm lớn này trở nên lớn hơn". Vì vậy, luật của Zipf vẫn tồn tại trong các cơ chế, trong đó các ưu tiên của các yếu tố được kết nối tích cực với quy mô nhóm (có nghĩa là, nhóm càng lớn thì càng có nhiều khả năng phát triển). Đây là lý do tại sao tôi thích nghĩ về các nhóm như các cụm và các yếu tố như các cụm.
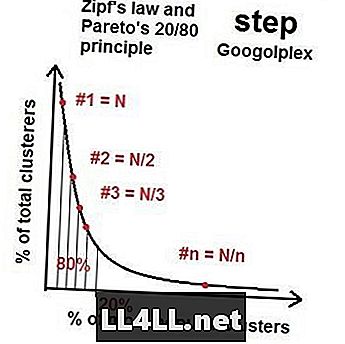
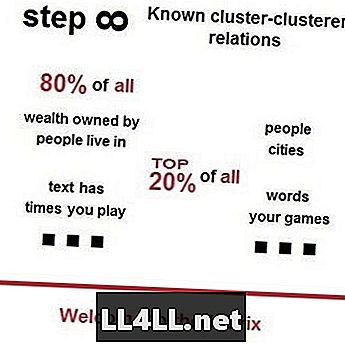
Luật của Zipf trên thị trường hơi nước
Nghi ngờ về điều cuối cùng? Dưới đây là lượng thời gian mọi người dành cho các trò chơi phổ biến nhất trên Steam .. Dữ liệu từ SteamSpy.
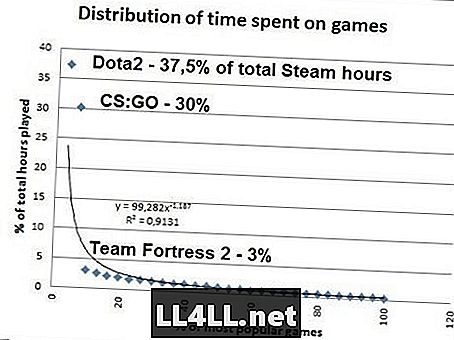
Nếu bạn làm toán, hóa ra 20% số trò chơi Steam phổ biến nhất chiếm 80% tổng số lần chơi, do đó, bí ẩn Pareto 20/80 hoạt động giống như một cơ duyên ở đây ... Tuy nhiên, phải chú ý Zipf là đúng, CS GO cần chiếm 37,5% / 2 = 18,8% tổng thời gian thay vì con số khổng lồ 30%. Nhưng ngoài điều này ngoại lệ (DỪNG CHƠI CS GO), phân phối giống như Zipf rõ ràng là có.
Dưới đây là số lượng bản sao được bán cho các trò chơi phổ biến nhất.
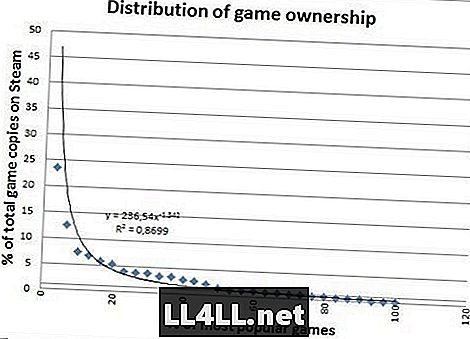
Trông đẹp hơn nhiều nhỉ? Các bản sao được bán không có các ngoại lệ lớn nên nó rất phù hợp, đó là một sự khác biệt đáng chú ý. Tuy nhiên, có một điều thú vị hơn để kết luận từ sự khác biệt của hai biểu đồ cuối cùng.
Bạn có để ý cách "cái đuôi" bên phải là loại chất béo trong biểu đồ thứ hai không? Nói một cách đơn giản, điều này cho chúng ta biết rằng các trò chơi "tương đối không phổ biến" thực sự phổ biến hơn rất nhiều so với cốt truyện trước đó.
Trên thực tế, hóa ra 20% các trò chơi phổ biến nhất chỉ chiếm 60% doanh thu, so với 80% khi chơi. Hấp dẫn? Bạn đặt cược mông của bạn nó là.
Chúng ta có thể học được gì về Steam?
Chà, thực tế là sự phổ biến của trò chơi tuân theo phân phối Pareto cho chúng ta biết rằng, thực sự có một loại hiệu ứng Mạng tích cực, khiến người chơi chọn các trò chơi đã được nhiều người chơi hơn. Điều khác biệt về độ béo của đuôi cho chúng ta biết là người dùng Steam thường "mù nhóm" hơn rất nhiều, khi mua game hơn so với khi họ chơi chúng.
Hãy suy nghĩ về điều đó - càng nhiều người mua trò chơi bất kể "ý kiến phổ biến hiện tại", thì việc phân phối Pareto càng được làm phẳng, vì ít có khả năng các trò chơi lớn sẽ phát triển hơn nữa. Nếu không ai đưa ra ý kiến về việc có bao nhiêu người đã chơi một trò chơi và tính khả dụng của tất cả các trò chơi là như nhau, thì chúng tôi sẽ mong đợi 20% các trò chơi phổ biến nhất chiếm khoảng 50% doanh số và thời gian chơi (ví dụ: giả sử sở thích cá nhân là phân phối chuẩn).
Kết luận
Vì vậy, có hai yếu tố góp phần vào việc phân phối Pareto trên thị trường Steam - nhà phát triển đổi mới như thế nào (có bao nhiêu miệng núi lửa mới được hình thành) và bao nhiêu game thủ (tiểu hành tinh) coi trọng quy mô nhóm hiện tại, khi chọn nhóm nào tham gia . Hóa ra, các game thủ rất mù nhóm khi mua game, nhưng ngược lại khi họ chơi chúng. Tuyệt không?
Nếu bạn muốn tìm hiểu thêm về các bản phân phối Luật và Quyền lực của Zipf, đây là một bài giảng hay. Hơn nữa, hãy chắc chắn có một cái nhìn vào bài báo của Newman!
Nếu bạn muốn đọc thêm các loại nội dung này, tôi sẽ sớm thử tham gia mô hình này cho một mô hình, điều này cho thấy các trò chơi nhiều người chơi phổ biến hơn có giá cao hơn (liên kết đến sở thích của game thủ để tham gia các nhóm có quy mô lớn hơn). Xem bài viết tại đây. Bài báo Piece De Kháng sẽ thử và kết hợp các lý thuyết này cùng nhau giải thích cách các trò chơi nhiều người chơi, mạng xã hội và thành phố trên thực tế là tất cả các hàng hóa chống đối thủ với hiệu ứng mạng, (càng nhiều người tiêu dùng tốt, càng có nhiều lợi ích của người tiêu dùng cá nhân) mang tên họ với màn sương bí ẩn Zipfian này ...
Cho đến lúc đó - hãy tận hưởng!
P.S. Đưa ra một nhận xét với một ý tưởng thú vị cho mối quan hệ 20/80 mà bạn nghĩ có thể đúng.
Tôi là:
80% nỗi nhớ của mọi người được gây ra bởi 20% những ký ức hạnh phúc nhất của họ (thực sự đã được chứng minh cho tỷ lệ mọi người quên thông tin tại)
80% khối lượng tập trung ở 20% các vật thể không gian lớn nhất (thực sự được chứng minh cho sự phân bố lực hấp dẫn)
Và dĩ nhiên
80% sự lộn xộn trong nhà vệ sinh của bạn đến từ 20% những gì bạn ăn (không có nghiên cứu học thuật nào để nói về)